최단 경로 알고리즘.
- 주요 알고리즘
- BFS (완전탐색 알고리즘)
- 가중치가 없거나 모든 가중치가 동일한 그래프에서 최단경로를 구하는 경우 가장 빠르다
- 다익스트라 알고리즘 (Dijkstra Algorithm)
- 음이 아닌 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm)
- 가중 그래프에서의 단일 쌍, 단일 출발, 단일 도착 최단 경로 문제
- 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
- 전체 쌍 최단 경로 문제, 다수출발, 단일도착
- 하나의 정점에서부터 다른 하나의 정점까지의 최단 경로를 구하는 경우
- A*알고리즘이 적합하다.
- BFS (완전탐색 알고리즘)
다익스트라
- 특정 노드에서 다른 모든 노드로 가는 최단경로를 갱신.
- 음의 간선이 없을 때 정상 동작. (그리디를 다르는 선택과 dp로 저장, 최신화 반복.)
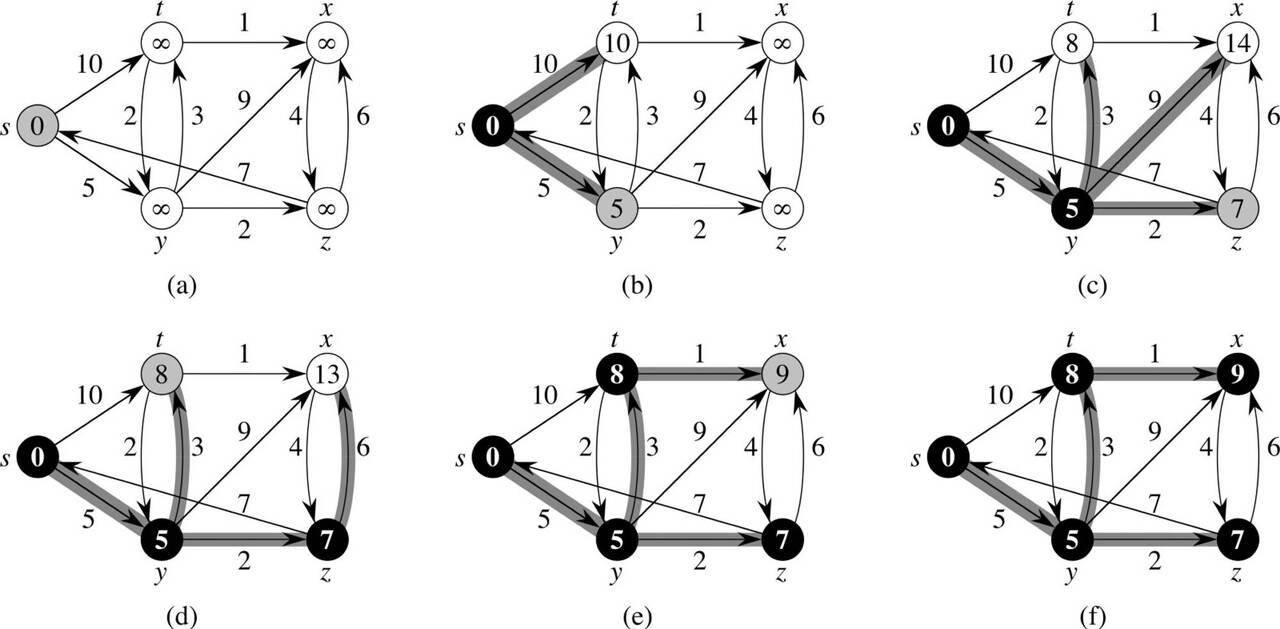
다익스트라 알고리즘의 동작 과정
- 현재 선택한 정점(처음엔 시작점)에 곧장 연결되고, 아직 방문하지 않은 정점들을 모두 본다.
- 선택한 정점과 보고있는 정점 사이의 거리와 시작 정점과 선택한 정점까지의 최단거리의 합이 현재까지 구한 시작 정점과 보고 있는 정점 사이의 거리보다 짧을 경우, 이를 갱신해준다.
- 1, 2번 수행이 모두 끝난 이후, 아직 방문하지 않은 정점들 중 시작점과의 거리가 가장 짧은 정점을 선택한다.
- 방문하지 않은 정점이 존재하여 정점을 선택했다면, 현재 구한 시작점으로부터의 현재 선택한 정점 사이의 거리는 최단거리이다.
- 방문하지 않은 정점이 존재하지 않는다면, 수행을 종료한다. 그렇지 않으면 1번으로 돌아가 수행을 반복한다.
다익스트라 알고리즘 특징
그리디 알고리즘 : 매상황에서 방문하지 않은 가장 비용이 적은 노드 선택
단계 거치며 한번 처리된 노드(이미 방문 처리)의 최단 거리는 고정되어 바뀌지 않음
- 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해
다익스트라 수행 후 , 테이블에 각 노드까지의 최단 거리 정보가 저장됨
단계마다 방문하지 않은 노드 중 최단 거리 가장 짧은 노드 선택하기 위해
매 단계마다 1차원 테이블의 모든 원소를 확인(순차 탐색)
순차 탐색 : 시간복잡도 O(N^2)
O(N)번에 걸쳐서 최단거리가 가장 짧은 노드 매번 선형탐색해야 하고, 현재 노드와 연결된 노드 매번 확인
전체노드개수가 5000이하라면 이렇게 풀 수 있으나 10000개넘어가면 해결 어려움
힙 자료구조 이용하는 다익스트라 알고리즘의 시간복잡도는 O(ElogV)
노드를 하나씩 꺼내 검사하는 반복문은 노드의 개수 V 이상의 횟수로는 처리되지 않음
- 결과적으로 현재 우선순위 큐에서 꺼낸 노드와 연결된 다른 노드들을 확인하는 총횟수는
최대 간선의 개수(E)만큼 연산이 수행될 수 있음(내부적으로 힙이 정렬해주기 때문에 )
직관적으로 전체 과정은 E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사
- 시간복잡도를 O(ElogE)로 판단 가능
- 중복 간선(양방향) 포함하지 않는 경우, 이를 O(ElogV)
- O(ElogE) -> O(ElogV^2) -> O(2ElogV) -> O(ElogV) ( 앞에 곱해진 2는 표기법에서 제거)
- 간선 개수 100,000개 , 노드 개수 10000개 까지는 1초안에 해결
- 로 정리
import heapq
# import sys
# input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수, 간선의 개수
n,m = map(int, input().split())
# 시작 노드 번호
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보 담는 리스트 만들기
graph = [[] for i in range(n+1)]
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n+1)
# 모든 간선 정보 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b,c))
def dijkstra(start):
q = []
# 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
# 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 련재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
# 현재 노드 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:# i[0] : 도착 노드임 , 햇갈리지 말자
distance[i[0]]= cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리 출력
for i in range(1, n+1):
# 도달할 수 없는 경우, 무한 이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리를 출력
else:
print(distance[i]) - 처음, 시작점을 제외한 모든 정점으로의 경로를 무한으로 한다.
- 선택한 정점(처음엔 시작점)으로부터 바로 이어진 정점으로의 경로를 구하고, 그 경로의 거리가 이어진 정점으로의 거리보다 작을 경우, 경로를 갱신해주면서 min heap에 추가한다.
- min heap의 top의 정점을 v라고 할 때에, v가 아직 선택하지 않은 정점일 때까지 heap에서 pop한다. v가 아직 방문하지 않은 정점이라면 그 정점에서부터 2번을 반복한다. 이 반복은 heap이 비어있지 않을 때까지 반복된다.
2. 플로이드 워셜
- 모든 노드에서 다른 모든 노드까지의 최단 경로.
- 매 단계마다 방문하지 않은 노드 중 최단거리 찾는 과정 필요x(우선순위큐 안써도됨.)
- 2차원 테이블에 최단거리 정보 저장.
- dp
- 각 단계마다 특정 노드 K 거쳐가는 경우 확인.min(A->B,A->K->B)


플로이드 워셜을 사용하는 문제는 노드의 개수가 500개 이하인 경우 대부분
-> 시간복잡도가 nn n 이므로 n=1000이라면 10억을 넘어간다
INF = int(1e9) # 무한을 의미하는 10억 설정
# 노드의 개수 및 간선의 개수 입력 받기
n = int(input())
m = int(input())
# 2차원 리스트를 만들고, 무한으로 초기화
graph = [[INF]*(n+1) for _ in range(n+1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n+1):
for b in range(1, n+1):
if a==b:
graph[a][b] = 0
# 각 간선에 대한 정보 입력받아, 그 값으로 초기화
for _ in range(m):
# a에서 b로 가는 비용은 c
a, b, c = map(int, input().split())
graph[a][b] = c
'''위에꺼 3개 한번에 처리
for(int i = 1; i<=n; i++){
for(int j =1; j<=n; j++){
if (i == j) dist[i][j] = 0;
else if (adj[i][j]) dist[i][j] = adj[i][j];
else dist[i][j] = INF;
}
}
'''
# 점화식에 따라 플로이드 워셜 수행
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k]+ graph[k][b])
# 수행된 결과 출력
for a in range(1, n+1):
for b in range(1, n+1):
# 도달할 수 없는 경우, 무한으로 출력
if graph[a][b] == INF:
print("INFINITY", end= ' ')
# 도달할 수 있는 경우 거리를 출력
else:
print(graph[a][b], end=' ')
print()플로이드 워셜 알고리즘 성능 분석
노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행
- 각 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려
- 총 시간 복잡도는 0(N^3)
3. 벨만-포드 알고리즘
음수 싸이클 없는 그래프에서 한정점 -> 모든 정점 최단경로 및 거리.
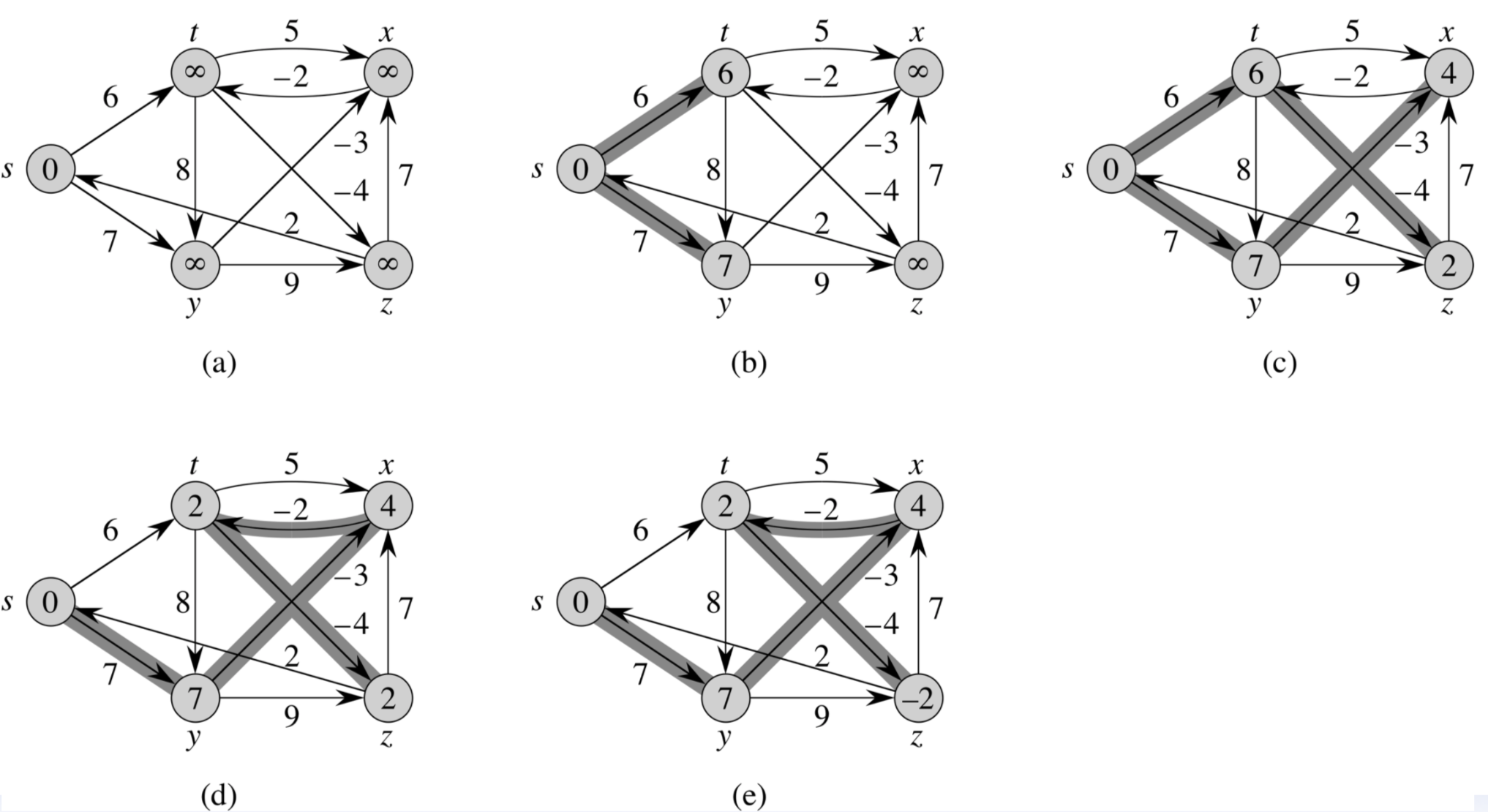
특징
- 음의 가중치를 가지는 간선도 가능하다.
- 음의 사이클의 존재 여부를 확인할 수 있다.
- 최단거리를 구하기 위해서 V-1번 E개의 모든 간선을 확인한다.
- 음의 사이클 존재 여부를 확인하기 위해서 한 번 더 E개의 간선을 확인한다.
- 총 연산횟수는 V*E이다. 따라서 시간복잡도는 O(VE)이다.
- V번째 모든 간선을 확인하였을 때 거리 배열이 갱신되었다면, 그래프 G는 음의 사이클을 가지는 그래프이다.
- 그래프 모든 엣지에 대해 edge relaxation을 시작노드를 제외한 전체 노드수 만큼 반복 수행한 뒤, 마지막으로 그래프 모든 엣지에 대해 edge relaxation을 1번 수행해 준다. 이때 한번이라도 업데이트가 일어난다면 음의 사이클이 존재한다는 뜻이 되어서 결과를 구할 수 없다는 의미의 false를 반환하고 함수를 종료한다.
INF = int(1e9)
def bf(start):
dis[start] = 0 # 시작 지점 초기화
# 매 반복마다 모든 간선 확인
# 음의 간선 사이클 존재 유무가 필요하면 n번과 return 처리
# 필요 없다면 n-1번과 리턴 처리는 필요 없음 dis 테이블만 필요함
for i in range(n):
# 모든 간선 확인
for j in range(m):
current = edges[j][0]
next_node = edges[j][1]
cost = edges[j][2]
# 시작위치에서 현재 노드까지 이동이 가능하면서
# 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은경우
if dis[current] != INF and dis[next_node] > cost + dis[current]:
dis[next_node] = dis[current] + cost
# 싸이클 유무 확인을 위해 n번 돌렸을 때
# 최단 거리 갱신이 발생하면 음의 사이클이 존재
if i == n - 1:
return True
return False
# 노드, 간선 개수
n, m = map(int, input().split())
edges = []
dis = [INF] * n # 최단 거리 테이블
# 간선 정보
for _ in range(m):
a, b, c = map(int, input().split())
edges.append((a, b, c))
cycle = bf(1)
if cycle: # 음의 사이클 발생
print(-1)
else:
# 1번 노드에서 시작했으니 다른 노드로 가기 위한 최단 거리 출력
for i in range(2, n + 1):
if dis[i] == INF:
print(-1)
else:
print(dis[i])
def bellman_ford(graph, start):
distance, predecessor = dict(), dict() # 거리 값, 각 정점의 이전 정점을 저장할 딕셔너리
# 거리 값을 모두 무한대로 초기화 / 이전 정점은 None으로 초기화
for node in graph:
distance[node], predecessor[node] = float('inf'), None
distance[start] = 0 # 시작 정점 거리는 0
# 간선 개수(V-1)만큼 반복
for _ in range(len(graph) - 1):
for node in graph:
for neighbour in graph[node]: # 각 정점마다 모든 인접 정점들을 탐색
# (기존 인접 정점까지의 거리 > 기존 현재 정점까지 거리 + 현재 정점부터 인접 정점까지 거리)인 경우 갱신
if distance[neighbour] > distance[node] + graph[node][neighbour]:
distance[neighbour] = distance[node] + graph[node][neighbour]
predecessor[neighbour] = node
# 음수 사이클 존재 여부 검사 : V-1번 반복 이후에도 갱신할 거리 값이 존재한다면 음수 사이클 존재
for node in graph:
for neighbour in graph[node]:
if distance[neighbour] > distance[node] + graph[node][neighbour]:
return -1, "그래프에 음수 사이클이 존재합니다."
return distance, predecessor
# 음수 사이클이 존재하지 않는 그래프
graph = {
'A': {'B': -1, 'C': 4},
'B': {'C': 3, 'D': 2, 'E': 2},
'C': {},
'D': {'B': 1, 'C': 5},
'E': {'D': -3}
}
# 그래프 정보와 시작 정점을 넘김
distance, predecessor = bellman_ford(graph, start='A')
print(distance)
print(predecessor)
# 음수 사이클이 존재하는 그래프
graph = {
'A': {'B': -1, 'C': 4},
'B': {'C': 3, 'D': 2, 'E': 2},
'C': {'A': -5},
'D': {'B': 1, 'C': 5},
'E': {'D': -3}
}
distance, predecessor = bellman_ford(graph, start='A')
print(distance)
print(predecessor)- 시작점을 제외한 모든 정점으로의 최단거리를 무한으로 설정한다(시작점은 0). 이후 다음 수행을 반복한다.
- 그래프 내에 모든 간선에 대해 2번을 시행한다.
- 정점 A에서 정점 B로의 방향을 가지고 있는 각 간선에 대해 현재 정점 B까지의 거리가 정점 A까지의 거리와 현재 간선의 거리의 합보다 클 경우, 정점 B의 경로와 거리를 갱신해준다.
- 이를 경로와 거리의 갱신이 일어나지 않을 때까지 반복해준다. 만약, 정점의 수 만큼의 시행 이후에도 경로와 거리의 갱신이 일어날 경우, 음수 사이클이 존재한다고 판단한다.
=> 정점의 수* 간선의 수 시행으로 최단경로를 구할 수 있다. 이상 탐색하면 음의사이클을 가지는 것
4. A* 알고리즘
F = 출발 지점에서 목적지까지 총 cost 합
G = 현재 노드에서 출발 지점까지의 총 cost
H = Heuristic(휴리스틱) : 현재 노드에서 목적지까지의 추정거리
F = G+H
4방향이면 좌표차이
8방향이면 이면 (좌표차이 피타고라스)
# Time Complexity는 H에 따라 다르다.
# O(b^d), where d = depth, b = 각 노드의 하위 요소 수
# heapque를 이용하면 길을 출력할 때 reverse를 안해도 됨
class Node:
def __init__(self, parent=None, position=None):
self.parent = parent
self.position = position
self.g = 0
self.h = 0
self.f = 0
def __eq__(self, other):
return self.position == other.position
def heuristic(node, goal, D=1, D2=2 ** 0.5): # Diagonal Distance
dx = abs(node.position[0] - goal.position[0])
dy = abs(node.position[1] - goal.position[1])
return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)
def aStar(maze, start, end):
# startNode와 endNode 초기화
startNode = Node(None, start)
endNode = Node(None, end)
# openList, closedList 초기화
openList = []
closedList = []
# openList에 시작 노드 추가
openList.append(startNode)
# endNode를 찾을 때까지 실행
while openList:
# 현재 노드 지정
currentNode = openList[0]
currentIdx = 0
# 이미 같은 노드가 openList에 있고, f 값이 더 크면
# currentNode를 openList안에 있는 값으로 교체
for index, item in enumerate(openList):
if item.f < currentNode.f:
currentNode = item
currentIdx = index
# openList에서 제거하고 closedList에 추가
openList.pop(currentIdx)
closedList.append(currentNode)
# 현재 노드가 목적지면 current.position 추가하고
# current의 부모로 이동
if currentNode == endNode:
path = []
current = currentNode
while current is not None:
# maze 길을 표시하려면 주석 해제
# x, y = current.position
# maze[x][y] = 7
path.append(current.position)
current = current.parent
return path[::-1] # reverse
children = []
# 인접한 xy좌표 전부
for newPosition in [(0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1)]:
# 노드 위치 업데이트
nodePosition = (
currentNode.position[0] + newPosition[0], # X
currentNode.position[1] + newPosition[1]) # Y
# 미로 maze index 범위 안에 있어야함
within_range_criteria = [
nodePosition[0] > (len(maze) - 1),
nodePosition[0] < 0,
nodePosition[1] > (len(maze[len(maze) - 1]) - 1),
nodePosition[1] < 0,
]
if any(within_range_criteria): # 하나라도 true면 범위 밖임
continue
# 장애물이 있으면 다른 위치 불러오기
if maze[nodePosition[0]][nodePosition[1]] != 0:
continue
new_node = Node(currentNode, nodePosition)
children.append(new_node)
# 자식들 모두 loop
for child in children:
# 자식이 closedList에 있으면 continue
if child in closedList:
continue
# f, g, h값 업데이트
child.g = currentNode.g + 1
child.h = ((child.position[0] - endNode.position[0]) **
2) + ((child.position[1] - endNode.position[1]) ** 2)
# child.h = heuristic(child, endNode) 다른 휴리스틱
# print("position:", child.position) 거리 추정 값 보기
# print("from child to goal:", child.h)
child.f = child.g + child.h
# 자식이 openList에 있으고, g값이 더 크면 continue
if len([openNode for openNode in openList
if child == openNode and child.g > openNode.g]) > 0:
continue
openList.append(child)
def main():
# 1은 장애물
maze = [[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
start = (0, 0)
end = (7, 6)
path = aStar(maze, start, end)
print(path)
if __name__ == '__main__':
main()
# [(0, 0), (1, 1), (2, 2), (3, 3), (4, 3), (5, 4), (6, 5), (7, 6)]공간복잡도
플로이드: V^2
다익스트라: V+E(인접리스트)
시간복잡도
플로이드: V^3
다익스트라: V^2(인접행렬), ElogV(인접리스트 + 우선순위 큐) ->
VlogV (피보나치힙이나 이진검색트리 사용, 하지만 이런 자료구조들은 상수가 커서 잘 안씀.)
장단점
- 플로이드 알고리즘 소스가 훨씬 더 간결하다.
- 플로이드 알고리즘은 간선 수가 많으면 다익스트라 알고리즘보다 빠를 수가 있음.
- 시작점으로부터 각 정점까지 최단거리만 구해도 될 때, 보통 다익스트라 알고리즘이 압도적으로 빠름.
- 그래프에 음의 가중치 간선이 있으면(물론 음의 싸이클은 없어야 한다) 다익스트라 알고리즘은 못 쓰지만 플로이드 알고리즘은 사용할 수 있다.
사용전략
- 정점간 최단경로를 모두 구해야 한다. 1-2. 간선이 많지 않다:
- 플로이드 알고리즘은 V^3, 다익스트라 알고리즘은 VElogV 경우에 따라 다름
- 1-1. 간선이 매우 많다(V^2=E): 플로이드 알고리즘이 우수함.
- 시작점으로부터 나머지 정점까지 최단거리만 구해도 된다. 2-2. 간선이 많지 않다: 인접리스트를 이용하는 다익스트라 알고리즘을 사용한다.
- 2-1. 간선이 매우 많다(V^2=E): 인접행렬을 이용하는 다익스트라 알고리즘을 사용한다.
- 최단경로를 구하는 것이 전체 시간에 큰 영향을 끼치지 않는다: 소스가 간결한 플로이드 알고리즘을 사용한다.
- 그래프 간선에 음의 가중치가 존재한다: 다익스트라 알고리즘은 무조건 사용하지 못한다. 다른 최단경로 알고리즘과 비교한다.
'practivceAlgorithm > 자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] 비트마스크???!!! (0) | 2021.07.29 |
|---|---|
| [자료구조] 이진트리와 탐색. 파이썬의 bisect (0) | 2021.07.25 |
| [알고리즘] 에라토스테네스의 체. (0) | 2021.07.21 |
| [알고리즘] 정렬 (0) | 2021.07.21 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2021.07.20 |