최소 신장 트리(MST, 크루스칼, 프림 알고리즘)
최소 신장 트리(Minnimum Spanning Tree)
- spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리.
- 신장 트리(Spanning Tree)란 그래프 내의 모든 정점을 포함하는 트리
- 최소 연결 : 간선의 수가 가장 적다.
- n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개 이고, (n-1)개의 간선으로 연결 되어이으면 필연적으로 트리형태가 되고 이게 신장 트리이다.
- 즉 그래프에서 일부 간선을 선택해서 만든 트리.
-
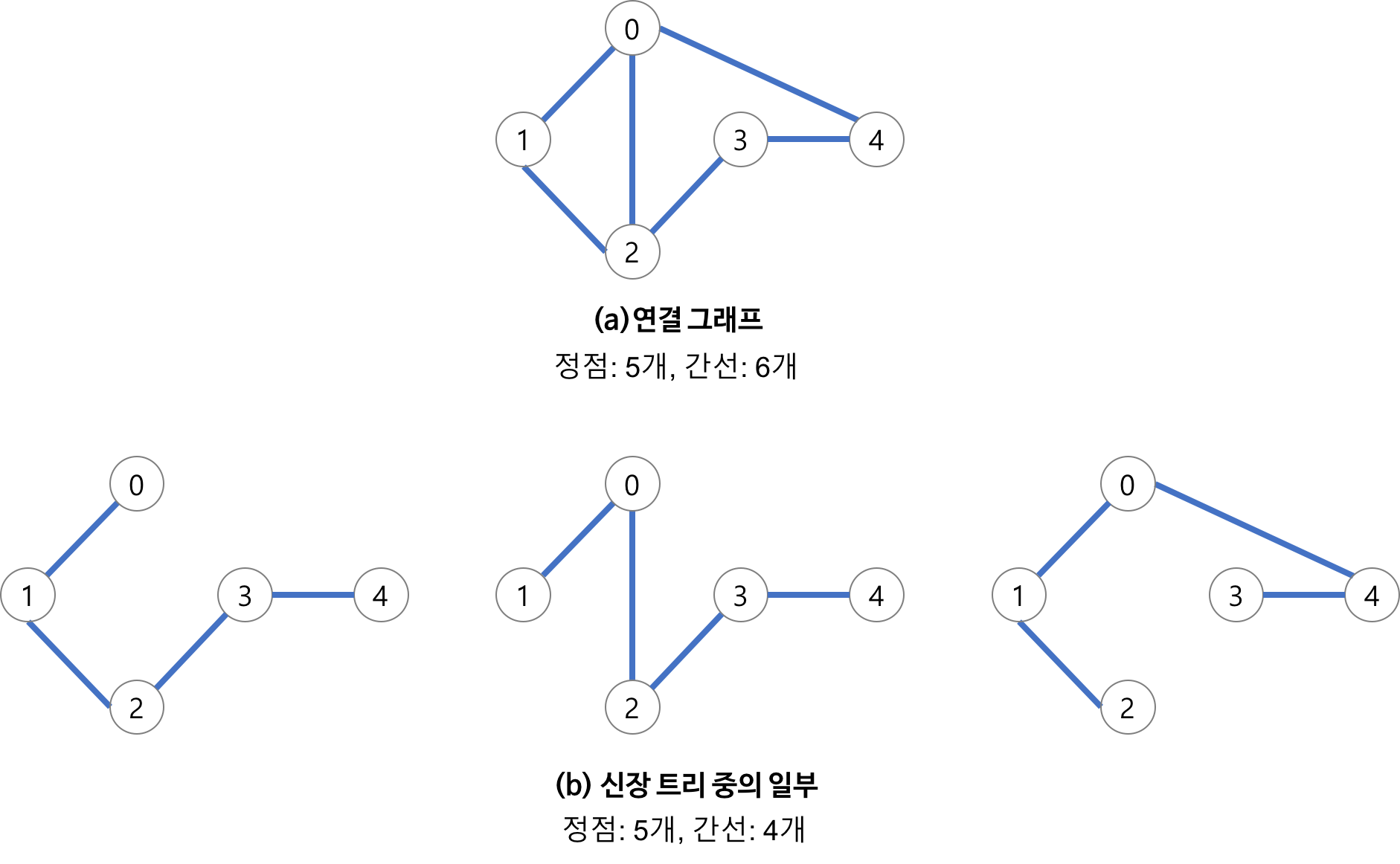
- DFS, BFS을 이용하여 그래프에서 신장 트리를 찾을 수 있다.
- 탐색 도중에 사용된 간선만 모으면 만들 수 있다.
- 하나의 그래프에는 많은 신장 트리가 존재할 수 있다.
- Spanning Tree는 트리의 특수한 형태이므로 모든 정점들이 연결 되어 있어야 하고 사이클을 포함해서는 안된다.
- 따라서 Spanning Tree는 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결 한다.
- Spanning Tree의 사용 사례
-통신 네트워크 구축-
- 신장 트리(Spanning Tree)란 그래프 내의 모든 정점을 포함하는 트리
예를 들어, 회사 내의 모든 전화기를 가장 적은 수의 케이블을 사용하여 연결하고자 하는 경우
n개의 위치를 연결하는 통신 네트워크를 최소의 링크(간선)를 이용하여 구축하고자 하는 경우, 최소 링크의 수는 (n-1)개가 되고, 따라서 Spanning Tree가 가능해진다.- MST는 "가중치를 고려" 하여 최소 비용의 스패닝 트리를 선택하는 것.
MST의 특징
- 간선의 가중치의 합이 최소여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
MST의 사용 사례
통신망, 도로망, 유통망에서 길이, 구축 비용, 전송 시간 등을 최소로 구축하려는 경우
- 도로 건설
- 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
- 전기 회로
단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제 - 통신
전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제 - 배관
파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제
MST의 구현 방법
Kruskal MST 알고리즘
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것 - 탐욕적 방법을 통해 문제를 해결하나 최적해라고 이미 증명된 알고리즘.
MST(최소 비용 신장 트리) 가
1) 최소 비용의 간선으로 구성됨
2) 사이클을 포함하지 않음 의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택 한다.
간선 선택을 기반으로 하는 알고리즘이다.
이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법이다.
[과정]
Kruskal의 알고리즘은 먼저 그래프의 e개의 간선들을 가중치의 오름차순으로 정렬한다. 정렬된 간선 리스트에서 순서대로 사이클을 형성하면 그 간선은 제외된다. 크루스칼 알고리즘이 어떻게 작동하는지 아래의 과정을 통해 살펴보자.
Kruskal의 알고리즘은 최소 비용 신장 트리를 구하는 다른 알고리즘보다 간단해 보인다. 하지만 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지를 체크하여야 한다. 새로운 간선이 이미 다른 경로에 의하여 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.
간선의 양끝 정점이 같은 집합에 속한다면 간선을 추가할 때 사이클이 형성된다. 하지만 양끝 정점이 서로 다른 집합에 속하는 경우 두 정점을 연결하여도 사이클이 형성되지 않는다. 따라서 지금 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 한다. 이 검사를 위한 알고리즘을 union-find 연산(알고리즘)이라 부른다.
# Union Find 연산
union-find 연산은 Kruskal 알고리즘에서만 사용되는 것이 아니라 일반적으로 널리 사용된다. union(x, y) 연산은 원소 x와 y가 속해 있는 집합을 입력으로 받아 2개의 집합의 합집합을 만든다. find(x) 연산은 원소 x가 속해 있는 집합을 반환한다.
예를 들어 S = { 1, 2, 3, 4, 5, 6 }의 집합을 가정하자. 먼저 집합의 원소를 하나씩 분리하여 독자적인 집합으로 만든다.
{ 1 }, { 2 }, { 3 }, { 4 }, { 5 }, { 6 }
여기에 union(1, 4)와 union(5, 2)를 하면 다음과 같은 집합으로 변화한다.
{ 1, 4 }, { 5, 2 }, { 3 }, { 6 }
또한 이어서 union(4, 5)와 union(3, 6)을 한다면 다음과 같은 결과를 얻을 수 있다.
{ 1, 4, 5, 2 }, { 3, 6 }
집합을 구현하는데는 여러가지 방법이 있을 수 있다. 비트 벡터, 배열, 연결 리스트 등을 이용하여 구현할 수 있다. 그러나 가장 효율적인 방법은 트리를 이용하는 것이다. 각 집합을 그 집합에 들어 있는 원소들의 트리로 표현한다. 집합은 트리의 루트에 의하여 대표된다. 예를 들어 집합 { 1, 4 }, { 5, 2 }, { 3 }, { 6 } 들은 아래의 그림의 (a) 와 같이 표현되고, 이어서 union(4, 5)와 union(3, 6)을 한다면 (b)와 같은 트리로 변화한다. 이 상태에서 find(4)를 한다면 루트인 정점 2가 집합의 대표로 반환된다.
find 연산에 소요되는 시간을 줄이려면 특정 정점과 루트와의 거리가 짧아야 한다. 모든 정점이 루트 아래에 있도록 구성한다면 소요시간을 줄일 수 있을 것이다. 이를 위하여 find 연산이 이루어질 때마다 모든 원소를 루트 노드 바로 밑에 놓는다. 또한 union 연산 시에 정점의 개수가 적은 트리의 루트가 큰 트리의 루트를 가리키도록 한다.
따라서 아래의 구현은 위 2가지를 염두에 두고 집합의 연산을 구현한 것이다. 여기서 트리는 포인터로 구현되는 것이 아니고 배열의 인덱스로 구현되어 있다. 배열의 인덱스를 포인터처럼 생각해본다. 트리는 부모의 정점을 가리키는 배열과 각 트리의 크기를 가지고 있는 배열 2개로 구성된다. 루트 정점은 부모 배열에서 -1을 가진다. // 루트의 부모는 없으므로 그 없는 정보를 단순히 -1로 표현하는 것뿐이다.
/*************************************************
** Union Find 연산의 구현
*************************************************/
int parent[MAX_VERTICES]; // 각 정점의 부모 노드
int num[MAX_VERTICES]; // 각 집합의 크기
// 초기화
void set_init(int n)
{
int i;
// 0 ~ n-1 인덱스까지 부모노드 배열은 모두 -1로
// 집합의 크기 배열은 모두 1로 초기화한다.
for (i = 0; i < n; i++)
{
parent[i] = -1;
num[i] = 1;
}
}
// 정점(vertex)이 속하는 집합을 반환한다.
int set_find(int vertex)
{
int p, s, i = -1; // p: 부모노드
// 루트노드까지 반복한다. p가 -1이 되면 반복문은 종료한다.
// p가 -1이라는 건 현재 노드(i)가 루트라는 뜻이다.
for (i = vertex; (p = parent[i]) >= 0; i = p);
s = i; // 루트노드 정보를 s에 저장
// 모든 노드들(i로 순회)의 부모가 s(루트 노드)에 되도록 설정한다.
for (i = vertex; (p = parent[i]) >= 0; i = p)
parent[i] = s;
return s; // 모든 노드의 부모인 루트를 반환한다.
}
// 두 개의 원소의 크기 정보 s1, s2를 받아 두 집합을 합친다.
void set_union(int s1, int s2)
{
// 더 큰 쪽을 기준으로 집합을 합친다.
if (num[s1] < num[s2])
{
// 집합 s2가 더 크다면
parent[s1] = s2; // s1의 부모를 s2로 설정
num[s2] += num[s1]; // s2의 크기를 s1만큼 더해준다.
}
else
{
parent[s2] = s1;
num[s1] += num[s2];
}
}
/*************************************************
** End Line
# Kruskal 알고리즘의 구현
위의 union 연산과 find 연산을 이용하여 Kruskal의 알고리즘을 구현해보면 아래와 같다. Kruskal 알고리즘에서는 간선들을 정렬하여야 하므로 최소 히프를 사용했다. 아래 프로그램이 그리고 있는 그래프는 위쪽에서 크루스칼 알고리즘의 작동원리를 설명할 때 사용했던 그래프다.
/*************************************************
** 최소히프를 이용한 Kruskal 알고리즘 (union find 포함)
*************************************************/
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100 // 그래프의 정점의 개수
#define INF 1000 // 경로가 존재하지 않음을 뜻함
#define MAX_ELEMENT 100 // 히프의 최대크기
/* union find*/
int parent[MAX_VERTICES]; // 각 정점의 부모 노드
int num[MAX_VERTICES]; // 각 집합의 크기
// 초기화
void set_init(int n)
{
int i;
// 0 ~ n-1 인덱스까지 부모노드 배열은 모두 -1로
// 집합의 크기 배열은 모두 1로 초기화한다.
for (i = 0; i < n; i++)
{
parent[i] = -1;
num[i] = 1;
}
}
// 정점(vertex)이 속하는 집합을 반환한다.
int set_find(int vertex)
{
int p, s, i = -1; // p: 부모노드
// 루트노드까지 반복한다. p가 -1이 되면 반복문은 종료한다.
// p가 -1이라는 건 현재 노드(i)가 루트라는 뜻이다.
// 우리는 위에서 루트노드의 부모는 -1로 설정했다.
for (i = vertex; (p = parent[i]) >= 0; i = p);
s = i; // 루트노드 정보를 s에 저장
// vertex의 조상노드들이 s(루트 노드)를 향하게끔 설정한다.
for (i = vertex; (p = parent[i]) >= 0; i = p)
parent[i] = s;
return s; // 모든 노드의 부모인 루트를 반환한다.
}
// 두 개의 원소의 크기 정보 s1, s2를 받아 두 집합을 합친다.
void set_union(int s1, int s2)
{
// 더 큰 쪽을 기준으로 집합을 합친다.
if (num[s1] < num[s2])
{
// 집합 s2가 더 크다면
parent[s1] = s2; // s1의 부모를 s2로 설정
num[s2] += num[s1]; // s2의 크기를 s1만큼 더해준다.
}
else
{
parent[s2] = s1;
num[s1] += num[s2];
}
}
typedef struct
{
int key; // 간선의 가중치
int u; // 정점 1
int v; // 정점 2
} element;
typedef struct
{
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
void init(HeapType *h)
{
h->heap_size = 0;
}
int is_empty(HeapType *h)
{
if (h->heap_size == 0)
return TRUE;
else
return FALSE;
}
void insert_min_heap(HeapType *h, element item)
{
int i = ++(h->heap_size);
/* 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정 */
// i가 루트가 아니고 입력으로 받은 item의 key값이 i의 부모의 키 값보다 작으면
while ((i != 1) && (item.key < h->heap[i / 2].key))
{
// 거슬러올라가야 하므로 현재노드를 부모노드로 설정하고
h->heap[i] = h->heap[i / 2];
// 인덱스를 부모노드의 인덱스로 설정한다.
i /= 2;
}
// 탈출했다는 건 더이상 거슬러 올라갈 곳이 없다는 것이므로
// 현재 인덱스의 위치에 item을 삽입한다.
h->heap[i] = item;
}
element delete_min_heap(HeapType *h)
{
int parent, child;
element item, temp;
// 최소히프의 특성상 루트노드에 있는 값이 가장 작은값이므로
// 반환할 루트노드의 값을 item에 저장해둔다.
item = h->heap[1];
// 맨 마지막에 있는 노드의 값을 temp에 저장하고
// 루트노드의 정보를 위에서 빼냈으므로 힙사이즈를 1 줄인다.
temp = h->heap[(h->heap_size)--];
/* 맨 마지막 노드값 (temp)를 이용한 비교과정 */
// temp를 일단 루트에 두었다고 가정하고 아래 과정을 시작한다.
// 최소히프 삭제는 루트노드부터 말단으로 가며 차례대로 비교하여
// 적절한 위치를 찾아 삽입하는 작업이다.
parent = 1; // 맨 첫 실행의 부모노드를 루트로 둔다.
child = 2; // 그리고 그 왼쪽 자식을 자식노드로 둔다.
// child가 힙 사이즈보다 크면 힙을 벗어난 비교이므로 실행이 안된다.
// 따라서 child가 힙 사이즈보다 작거나 같을 때 비교가 일어난다.
while (child <= h->heap_size)
{
// 두 개의 자녀 중 더 작은 자녀를 비교기준으로 삼기 위해 아래의 if문 실행
if (
// 오른쪽 자녀가 있다고 생각하면, child는 힙사이즈보다 작아야 한다.
// 왼쪽 자녀가 힙사이즈와 같은데 오른쪽 자녀가 있다면 + 1을 해줘야 하는데
// 그렇게 되면 힙사이즈를 넘어서기 때문에 child는 힙사이즈보다 작아야 한다.
(child < h->heap_size) &&
// 오른쪽 자녀 (child + 1)이 더 작기 때문에 새로운 기준점을 만들어주기 위해
// child++ 을 해준다.
(h->heap[child].key) > h->heap[child + 1].key
)
child++;
// 비교 대상인 child를 설정했으니 루트노드에 위치 중인 temp와 비교한다.
// temp가 더 작다면 위치이동을 할 필요가 없으므로 이 반복문을 빠져나간다.
// 제자리에 있다는 뜻이다. 최소히프는 작은 값이 부모로 있어야 한다.
if (temp.key <= h->heap[child].key)
break;
// 여기까지 왔다는 건 temp의 자리교환이 필요하다는 뜻이다.
// temp가 있을 곳을 찾기 위해 비교대상을 한 단계 아래로 이동한다.
h->heap[parent] = h->heap[child]; // 자녀의 값이 새로운 비교 기준점이 된다.
parent = child; // 자녀가 부모로 된다. (다음 비교를 위해)
child *= 2; // 2를 곱하여 다음 자녀로 된다.
}
// 위 반복문을 빠져나오면, parent가 temp가 위치할 곳이 되어 있을 것이다.
h->heap[parent] = temp;
return item;
}
void insert_heap_edge(HeapType *h, int u, int v, int weight)
{
element e;
e.u = u;
e.v = v;
e.key = weight;
insert_min_heap(h, e);
}
void insert_all_edges(HeapType *h) // 직접 그림을 그려보면 편하다.
{
// 최소히프이므로 가장 작은 노드가 루트노드로 위치하게 된다.
insert_heap_edge(h, 0, 1, 29);
insert_heap_edge(h, 1, 2, 16);
insert_heap_edge(h, 2, 3, 12);
insert_heap_edge(h, 3, 4, 22);
insert_heap_edge(h, 4, 5, 27);
insert_heap_edge(h, 5, 0, 10);
insert_heap_edge(h, 6, 1, 15);
insert_heap_edge(h, 6, 3, 18);
insert_heap_edge(h, 6, 4, 25);
}
// kruskal의 최소 비용 신장 트리 알고리즘
void kruskal(int n)
{
int edge_accepted = 0; // 현재까지 선택된 간선의 수
HeapType h; // 최소 히프
int uset, vset; // 정점 u와 정점 v의 집합 번호
element e; // 히프 요소
init(&h); // 히프 초기화
insert_all_edges(&h); // 히프에 간선들을 삽입
set_init(n); // 집합 초기화
while (edge_accepted < (n - 1)) // 간선의 수 < (n - 1)
{
e = delete_min_heap(&h); // 가장 작은 가중치의 간선 획득
// 획득됨과 동시에 해당 간선은 히프에서 제거된다.
uset = set_find(e.u); // 정점 u의 집합 번호
vset = set_find(e.v); // 정점 v의 집합 번호
// 두 집합이 서로 다른 집합에 속한다면
if (uset != vset)
{
printf("(%d, %d) %d \n", e.u, e.v, e.key);
edge_accepted++;
set_union(uset, vset); // 두 개의 집합을 합친다.
}
}
}
void main()
{
kruskal(7);
}
/*************************************************
** End Line
*************************************************/
</stdio.h>
파이썬 코드(크루스칼)
arent = dict()
rank = dict()
# 비방향 그래프 임을 확인 (방향그래프도 가능하다)
graph = {
'vertices': ['v1','v2','v3','v4','v5'],
'edges' : [(1,'v1','v2'),
(3,'v1','v3'),
(3,'v2','v3'),
(6,'v2','v4'),
(4,'v3','v4'),
(5,'v4','v5'),
(2,'v3','v5')]
}
def find(node):
# path compression 기법
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node_v, node_u):
root1 = find(node_v)
root2 = find(node_u)
# union-by-rank 기법
if rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2] += 1
def make_set(node):
parent[node] = node
rank[node] = 0
def kruskal(graph):
mst = list()
# 1. 초기화 그래프의 모든 node에 대해 개인을 가지는 집합 생성.
for node in graph['vertices']:
make_set(node)
# 2. 간선 weight(가중치) 기반 오름차순 sorting
edges = graph['edges']
edges.sort()
# 3. 간선 연결 (사이클 없는)
for edge in edges:
weight, node_v, node_u = edge
# 노드v와 u가 연결되어 있지 않다면? 연결한다!
# 연결하고 최소신장트리 집합의 간선에 넣는다.
if find(node_v) != find(node_u):
union(node_v, node_u)
mst.append(edge)
print('mst:', mst)
return mst
print(kruskal(graph))Prim MST 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장 해나가는 방법
정점 선택을 기반으로 하는 알고리즘이다.
이전 단계에서 만들어진 신장 트리를 확장하는 방법이다.
(이전 단계까지 만들어진 신장트리 집합에 인접한 정점들 중 최소 간선으로 연결 된 정점을 선택해 트리를 확장한다.)
=> 이전 단계에서 만들어진 신장 트리 정보를 활용하므로 저장할 필요가 있다.
(트리가 n-1가넌을 가질때까지 계속된다.)
[과정]
시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
즉, 가장 낮은 가중치를 먼저 선택한다.
위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.
Prim 알고리즘을 이해하는 첫 단추는 프로그래밍 언어가 아닌 손으로 풀어가는 과정을 겪는 것이다. 아래의 과정을 직접 그려보는 것이 Prim 알고리즘을 이해하는 데 도움을 줄 것이다.
#1 시작점을 0번 정점으로 설정해둔 후에 각 정점까지의 거리가 얼마인지 적는다. 무한대로 표시되어 있는 것은 바로 가는 경로가 없고 어딘가를 거쳐서 가야함을 뜻한다. 우리는 직접적으로 연결되어 있는 정점의 거리만 표시한다. 표시한 거리 중 가장 짧은 거리는 0번 정점과 4번 정점의 거리인 3이다. 따라서 첫 번째 경로인 0 - 4 경로(간선)을 찾았다.
#2 기존의 경로인 0 - 4를 기준으로 두고 생각해보자. 4번 정점을 기준으로 새롭게 나아갈 수 있는 곳들의 거리를 표시해보자. 4번정점에서는 1번 정점, 그리고 6번 정점으로 갈 수 있으므로 각 거리를 적어준다. 그 중에서 1번 정점까지의 거리가 가장 짧으므로 1번 정점을 택한다. 이로서 1- 4의 경로가 선택됐다.
#3 이번에는 1번 정점에서 어디로 나아갈 수 있는지를 찾아본다. 2번과 3번, 그리고 5번으로 나아갈 수 있다. 여기서 5번 정점을 주목해보자. 이미 길이가 10인 경로가 존재했지만, 1번 정점을 통하면 거리가 6으로 줄어든다. 우린 최소경로를 찾고 있는 것이기 때문에 이렇게 더 짧은 경로가 발견되면 그 정보를 갱신해준다.
이미 선택된 최소경로를 제외하면, 새롭게 나아갈 곳 중 가장 짧은 경로는 1 - 2 경로다. 따라서 2번 정점을 선택한다.
#4 위에서 선택한 2번을 토대로 갱신할 수 있는 경로 혹은 새롭게 나아갈 수 있는 경로가 있는지 탐색한다. 새롭게 나아갈 수 있는 경로는 없었지만, 갱신할 수 있는 정보가 있다. 2번에서 3번 경로가 기존의 10길이에서 2길이로 줄어드므로 갱신해준다. 그 후 현재까지 선택된 경로 중 가장 거리가 짧은 경로인 2 - 3 경로를 선택해준다. 이로써 3번 정점이 선택됐다.
#5 위에서 선택한 3번 정점을 토대로 새로얻을 수 있는 정보는 3 - 6 경로의 거리 정보다. 기존의 길이인 5보다 더 짧은 4가 나오므로 정보를 갱신해준다. 그 후 지금까지 선택된 정점을 제외한 것 중 가장 짧은 경로인 3 - 6 경로를 선택한다. 즉 우리는 6번 정점을 선택한 것이다.
#6 마지막이다. 지금까지의 경로 중 선택되지 않은 정점은 5번 정점이다. 5번 정점을 선택하고 새롭게 갱신할 수 있는 정보가 있는지 살펴본다. 없다. 5번 정점의 거리는 1번 정점을 선택할 때 나온 것이므로, 1 - 5의 경로가 선정됐다. 이로써 Prim 알고리즘의 종료다. MST에 적어둔 경로들로 종합한 것이 그래프의 최단 경로다.
#7 Prim을 직접 손으로 작성해보고, 그 결과인 간선들을 토대로 탄생한 최소 신장 그래프는 아래의 그래프다.
# Prim의 알고리즘 구현
먼저 dist라는 정점의 개수 크기의 배열이 필요하다.
dist는 현재까지 알려진 신장트리의 정점 집합에서 각 정점까지의 거리를 가지고 있다.
처음에는 시작 노드만 값이 0이고, 다른 노드는 전부 무한대(프로그램에서는 1000L)의 값을 갖는다.
아직까지 트리집합에는 아무것도 존재하지 않는다.
정점들이 트리 집합에 추가되면서 dist(가중치)의 값은 변경된다.
여기서 우선순위 큐(heapq)를 하나 도입한다. 배열로 구현할 수도 있고 히프를 통해 구현할 수도 있다.
우선순위 큐에 모든 정점을 삽입한다. 이 때의 우선순위는 dist 배열값이 된다.
다음은 while 루프로 우선순위큐에서 가장 작은 dist값을 가지는 정점을 추출한다.
(첫 실행때는 시작 정점인 0이 추출될 것이다.) 추출된 정점이 트리 집합에 추가된다.
프로그램에서 추가의 구현은 화면에 출력하는 것으로 했다.
다음에는 트리 집합에 새로운 정점 u가 추가되었으므로 u에 인접한 정점 v들의 dist값을 변경시켜준다.
즉 기존의 dist[v] 값보다 간선 (u, v)의 가중치가 적으면 간선 (u, v)의 가중치로 dist[v]를 변경시킨다.
우선순위큐에 있는 모든 정점들이 소진될 때까지 이러한 과정을 되풀이하면 된다.
한 번 선택된 정점은 Q에서 삭제되므로 다시 선택되지는 않는다.
그리고 트리 집합에 인접하지 않는 정점들의 dist 값은 무한대이므로 역시 선택되지 않을 것이다. 아래는 프로그램 코드다. 코드를 간단히 하기 위하여 오류 처리가 생략되었는데, 만약 알고리즘 도중에 선택된 정점의 dist 값이 무한대이면 오류처리가 된다. 왜냐하면 우린 최소 신장 트리를 구하고 있고 그 과정이 반드시 인접한 정점을 선택하는 것이 되어야 하기 때문이다.
/*************************************************
** Prim의 최소 비용 신장 트리 프로그램
*************************************************/
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 7 // 신장트리의 정점 개수
#define INF 1000L // 경로가 없는 INFINITE를 표현하기 위해 정의된 상수 INF
int weight[MAX_VERTICES][MAX_VERTICES] = {// 신장트리의 거리와 모양을 배열로 표현, INF는 바로갈 수 있는 경로가 없음을 뜻한다.
{0,29,INF,INF,INF,10,INF},
{29,0,16,INF,INF,INF,15},
{INF,16,0,12,INF,INF,INF},
{INF,INF,12,0,22,INF,18},
{INF,INF,INF,22,0,27,25},
{10,INF,INF,INF,27,0,INF},
{INF,15,INF,18,25,INF,0}
};
int selected[MAX_VERTICES]; // 선택된 정점의 정보를 담을 배열, 선택이 됐는지 안됐는지를 표시한다.
int dist[MAX_VERTICES]; // 최소의 거리 정보만을 담는 배열, 새로운 최소거리가 나올 때마다 갱신된다.
// 최소 dist[v]값을 갖는 정점을 반환
int get_min_vertex(int n)
{
int v, i; // 정점의 정보를 저장할 변수 v, 반복문을 위한 변수 i
for (i = 0; i < n; i++)
{
if (selected[i] == FALSE) {
v = i; // 아직 선택되지 않은 정점의 번호를 v에 저장, 각 함수 실행별 0부터 n - 1까지 차례대로 저장된다.
break;
}
}
// 위에서 선택된 정점이 과연 최소거리를 지니고 있는 정점인지를 확인한다.
for (i = 0; i < n; i++)
{
// 선택되지 않은 정점들을 순회하면서 최소거리를 가진 정점을 찾아낸다.
if (selected[i] = FALSE && (dist[i] < dist[v]))
v = i; // 더 적은 거리가 존재한다면 해당 정점을 저장한다.
}
return(v); // 최소의 거리를 갖는 정점이 선택됐으므로 정점 번호를 리턴한다.
}
// Prim, s는 시작 정점
void prim(int s, int n)
{
int i, u, v;
for (u = 0; u < n; u++) // dist배열과 selected배열의 정보를 초기화
{
dist[u] = INF;
selected[u] = FALSE;
}
dist[s] = 0; // 시작정점과 시작정점간의 거리는 0이다. 자기자신을 순환하는 경로는 없다고 가정한다.
for (i = 0; i < n; i++)
{
// 리턴된 정점 번호를 u에 저장한다. u는 최소거리를 가지는 정점. 손으로 썻을 때 선택하는 효과를 가져온다.
u = get_min_vertex(n);
selected[u] = TRUE; // 최소거리를 갖는 정점의 정보(u)를 알아냈으니 해당 정점을 선택했다고 표시한다.
// 만약 경로가 없다면 함수를 종료한다. 정상적인 신장트리의 정보가 들어왔다면 실행될 일은 없을 것이다.
if (dist[u] == INF) return;
printf("%d ", u); // 방문한 정점(u)을 출력한다.
for (v = 0; v < n; v++) // 이 과정은 우리가 새롭게 발견한 정보를 저장하는 과정이다.
// 직접적인 경로가 발견되어 INF 에서 상수거리로 바뀌는 과정과
// 기존의 상수거리보다 더 짧은 거리가 발견되 그 정보를 갱신하는 과정이 포함되어 있다.
{
// 선택된 u 정점을 기준으로 정점(u)과 연결되어 있는 정점까지의 거리를 각각 비교한다.
if (weight[u][v] != INF) // 정점 u와 연결이 되어있고
{
// 아직 선택되지 않았으며 해당 변(weight[u][v])의 길이가 기존의 dist[v] 값보다 작다면
if (selected[v] == FALSE && weight[u][v] < dist[v])
dist[v] = weight[u][v]; // dist[v]의 값을 갱신해준다.
// 새롭게 발견되는 정점들이 초반에 저장될 수 있는 건 INF를 1000으로 설정해줬기 때문이다.
// 우리가 만든 그래프의 경로값들은 전부 100이하의 값이기 때문에 새롭게 발견되는 정점이 있다면
// 우선 등록되고 그 후 더 짧은 거리가 등장하면 갱신되는 형태로 이 프로그램은 작동한다.
}
}
}
}
void main()
{
prim(0, MAX_VERTICES); // 정점 개수가 7개인 그래프에서 0번 정점을 출발하여 얻을 수 있는 최소비용신장트리를 찾아라.
}
/*************************************************
** End Line
*************************************************/
파이썬 코드(프림)
"""
주어진 인접행렬에서, Prim 알고리즘을 통해 최소 신장 트리를 구한다.
입력: 인접 행렬, 시작 정점
출력: 시작 정점에서 만든 최소 신장 트리
알고리즘:
1. dist 배열을 INF로 초기화
2. dist[start] = 0
3. 우선 순위 큐 queue에 모든 정점 삽입(우선 순위는 dist[])
4. i는 0부터 n-1까지 반복
1). u에 weight가 가장 작은 간선 삽입
2). u의 인접 정점들인 v를 반복
v가 Q의 원소이고, weight[u][v] < dist[v]라면
dist[v]에 weight[u][v]를 할당
설명:
0. 프림 알고리즘은 시작 정점을 최초의 신장 트리로 놓는다.
1. 시작 정점만이 포함된 신장 트리에서, 더 포함시킬 수 있는 노드들을 찾아놓는다.
2. 더 포함시킬수 있는 노드 중, 비용(가중치)가 가장 작은 노드를 포함시킨다.
3. 2에서 포함된 정점에서 가장 낮은 비용으로 도달할 수 있는 노드를 찾아서,
그 노드를 신장 트리에 포함시킨다.
"""
INF = 999
adj_mat = [[0, 29, INF, INF, INF, 10, INF],
[29, 0, 16, INF, INF, INF, 15],
[INF, 16, 0, 12, INF, INF, INF],
[INF, INF, 12, 0, 22, INF, 18],
[INF, INF, INF, 22, 0, 27, 25],
[10, INF, INF, INF, 27, 0, INF],
[INF, 15, INF, 18, 25, INF, 0]]
node_num = len(adj_mat)
visited = [False] * node_num
distances = [INF] * node_num
"""
get_min_node 메소드
1. i가 0부터 node 갯수만큼 반복한다.
i 노드가 방문한 적 없는 노드라면,
v에 i를 저장한다.
멈춘다.
2. i가 0부터 node_num 만큼 반복한다.
i가 방문하지 않았고, 방금 저장한 v보다 비용이 작은(기존의 신장트리로부터의 거리가 작은)
노드 i를 발견한다면
v에 i를 덮어쓴다.
v를 리턴한다.
"""
def get_min_node(node_num):
print("get_min_node 함수 진입했다")
for i in range(node_num):
if not visited[i]:
v = i
break
print("아직 방문하지 않은 v: ", v)
for i in range(node_num):
if not visited[i] and distances[i] < distances[v]:
print("i: ", i, "\tv: ", v)
print("distaces[i], distances[v]: ", distances[i], distances[v])
v = i
print("아직 방문 안됐고, 기존 v보다 distances값 작은 정점 발견 교체, 최종 v: ", v)
return v
def prim(start, node_num):
# distances 배열과 visted 배열 초기화
for i in range(node_num):
visited[i] = False
distances[i] = INF
# 시작노드의 distance 값을 0으로 초기화
distances[start] = 0
for i in range(node_num):
print("--------------------")
print("prim 메소드 내부 반복 시작, 반복 회차: ", i)
node = get_min_node(node_num)
visited[node] = True # node 를 방문했다 표시
print("\nget_min_node 에서 선택된 노드: ", node)
for j in range(node_num):
if adj_mat[node][j] != INF:
if not visited[j] and adj_mat[node][j] < distances[j]:
print("방금 포함된 ", node, "와 연결되어있고, "
"아직 방문하지 않았으며, "
"기존의 신장트리로부터의 거리보다 작은 경로가 발견되어, "
"distances[j]의 값을 갱신해야 하는 j: ", j)
distances[j] = adj_mat[node][j]
print("distances: ", distances)
print("--------------------")
print(prim(0, node_num))
print("distances: ", distances)
print("minimum cost: ", sum(distances))Prim & Kruskal 알고리즘의 시간 복잡도
프림 알고리즘은 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하고, union-find 알고리즘을 이용하면 Kruskal 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다.
즉, 간선 e개를 퀵 정렬과 같은 효율적인 알고리즘으로 정렬한다면
Prim의 알고리즘의 시간 복잡도는 O(n^2) 이 된다.
Kruskal 알고리즘의 시간 복잡도는 O(elog₂e) 이므로
그래프 내에 적은 숫자의 간선만을 가지는 ‘희소 그래프(Sparse Graph)’의 경우 Kruskal 알고리즘이 적합하고
그래프에 간선이 많이 존재하는 ‘밀집 그래프(Dense Graph)’ 의 경우는 Prim 알고리즘이 적합하다.
크루스칼 VS 프림
- 프림은 정점 위주의 알고리즘, 크루스칼은 간선 위주의 알고리즘
- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 트리르 구성 하므로 그 과정에서 사이클을 이루지 않지만 크루스칼은 시작점을 따로 정하지 않고 최소 비용의 간선을 차례로 대입 하면서 트리를 구성하기 때문에 사이클이 이루어지는 항상 확인 해야한다.
- 프림의 경우 최소 거리의 정점을 찾는 부분에서 자료구조의 성능에 영향을 받는다.
- 크루스칼은 간선을 기준으로 정렬하는 과정이 오래 걸린다.
- 간선의 개수가 작은 경우에는 크루스칼, 간선의 개수가 많은 경우에는 프림.
더 자세히 공부하고 싶으면 참고
https://victorydntmd.tistory.com/102?category=686701
복제로봇 나중에 풀어보기
https://www.acmicpc.net/problem/1944
1944번: 복제 로봇
첫째 줄에 미로의 크기 N(4 ≤ N ≤ 50)과 열쇠의 개수 M(1 ≤ M ≤ 250) 이 공백을 사이에 두고 주어진다. 그리고 둘째 줄부터 N+1째 줄까지 미로의 정보가 주어진다. 미로는 1과 0, 그리고 S와 K로 주어
www.acmicpc.net
참고
- 신장 트리 https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
- 프림 알고리즘https://mattlee.tistory.com/46 [waca's field]
- 크루스칼 출처: https://mattlee.tistory.com/47?category=683544 [waca's field]
- https://godls036.tistory.com/26
'practivceAlgorithm > 자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] 에라토스테네스의 체. (0) | 2021.07.21 |
|---|---|
| [알고리즘] 정렬 (0) | 2021.07.21 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2021.07.20 |
| [알고리즘] 분할정복(Divide Conquer) (0) | 2021.07.17 |
| [자료구조] 유니온-파인드(union-find) (0) | 2021.07.09 |

















