펜윅 트리(바이너리 인덱스 트리)
시간복잡도 O(MlogN)
구간합, 값 업데이트O(logN)
 그림1. 세그먼트 트리
그림1. 세그먼트 트리
 그림2. 펜윅 트리
그림2. 펜윅 트리
Fenwick Tree를 구현하려면 어떤 수 X를 이진수로 나타냈을 때 마지막 1의 위치를 알아야 합니다.
마지막 1이 나타내는 값을 L[i]라고 표기하면 L[3]은 11(2)로 1, L(10)은 1010(2)로 2 가 됩니다.
수 N개를 A[1] ~ A[N] 이라고 했을 때, Tree[i]는 A[i] 부터 앞으로 L[i] 개의 합이 저장되어 있습니다.
아래 그림은 각각의 i에 대해서, L[i]를 나타낸 표입니다. 아래 초록 네모는 i부터 앞으로 L[i]개가 나타내는 구간입니다.

L[i] = i & -i가 됩니다. 그 이유는 아래와 같습니다.
-num = ~num + 1
num = 100110101110101100000000000
~num = 011001010001010011111111111
-num = 011001010001010100000000000
num & -num = 000000000000000100000000000A = [3, 2, 5, 7, 10, 3, 2, 7, 8, 2, 1, 9, 5, 10, 7, 4]인 경우에, 각각의 Tree[i]가 저장하고 있는 값은 다음과 같게 됩니다.

예를 들어, Tree[12]에는 12부터 앞으로 L[12] = 4개의 합은 A[9] + A[10] + A[11] + A[12]가 저장되어 있습니다. Tree[7]에는 7부터 앞으로 L[7] = 1개의 합인 A[7]이 저장되어 있습니다.
위 그림에 모든 것이 설명되어 있긴 하지만, 자세히 살펴보자. i는 0 이상인 정수이다.
인덱스가 홀수인 원소는 수열의 해당 인덱스의 값을 그대로 가진다.
- data[2i+1]=arr[2i+1]data[2i+1]=arr[2i+1]
- data[1] = arr[1], data[3] = arr[3], …
인덱스가 2의 배수이면서 4의 배수가 아닌 원소(2, 6, 10, 14, …)는 직전 두 arr 원소의 합을 보존한다.
- data[4i+2]=arr[4i+1]+arr[4i+2]data[4i+2]=arr[4i+1]+arr[4i+2]
- data[2] = arr[1] + arr[2], data[6] = arr[5] + arr[6], …
인덱스가 2^k의 배수이면서 2^(k +1)의 배수가 아닌 원소는 직전 arr의 2^k개의 값의 합을 보존한다.
data[12]는 2^2의 배수이면서 2^3의 배수가 아니므로 arr[9] + arr[10] + arr[11] + arr[12]의 값을 저장한다.
비트 연산을 이해한다면 구현도 굉장히 쉽다. 구체적인 예(arr[1…43])를 보자.
- arr[1…43] = data[32] + data[40] + data[42] + data[43]이다.
- 43을 이진법으로 나타내면 101011(2)이다.
- 43의 LSB(1인 비트 중 끝자리)를 하나 뗀다. 101010(2)=42이다.
- 하나 더 떼 본다. 101000(2)=40이다.
- 하나 더 떼 본다. 100000(2)=32이다
그럼 LSB를 어떻게 쉽게 구하는가?
- idx = 43으로 두고, idx &= idx – 1 연산을 idx가 0이 될 때까지 수행한다.
- 이게 왜 되는지 이해가 안 된다면 idx와 idx - 1을 이진법으로 나타내고, and 연산을 수행해보면 이해가 될 것이라 장담한다.
- 사실 LSB 자체를 구하는 것은 업데이트 연산에서 볼 수 있듯이 (idx & -idx)로 구할 수 있다. 하지만 LSB를 빼는 것은 idx &= idx - 1로도 가능하다.
합 구하기
Tree를 이용해서 A[1] + ... + A[13]은 어떻게 구할 수 있을까요?
13을 이진수로 나타내면 1101입니다. 따라서, A[1] + ... + A[13] = Tree[1101] + Tree[1100] + Tree[1000]이 됩니다. Tree의 인덱스는 이진수입니다.

1101 -> 1100 -> 1000는 마지막 1의 위치를 빼면서 찾을 수 있습니다. 이것을 코드로 작성해보면 다음과 같습니다.
int sum(int i) {
int ans = 0;
while (i > 0) {
ans += tree[i];
i -= (i & -i);
}
return ans;
}모든 i에 대해서, A[1] + ... + A[i]를 구하는 과정을 그림으로 나타내면 다음과 같습니다.

어떤 구간의 합 A[i] + ... + A[j]는 A[1] + ... + A[j]에서 A[1] + ... + A[i-1]을 뺀 값과 같습니다. 따라서, sum(j) - sum(i-1)을 이용해서 구할 수 있습니다.
변경
어떤 수를 변경한 경우에는, 그 수를 담당하고 있는 구간을 모두 업데이트해줘야 합니다. 아래와 같이 마지막 1의 값을 더하는 방식으로 구현할 수 있습니다.
- 인덱스 7 업데이트
- 00111(2) = 7
- 00111(2) + 00001(2) = 01000(2) = 8
- 01000(2) + 01000(2) = 10000(2) = 16
void update(int i, int num) {
while (i <= n) {
tree[i] += num;
i += (i & -i);
}
}아래 그림은 i를 변경했을 때, 바꿔줘야하는 Tree[i]를 나타낸 그림입니다.

2042번 문제: 구간 합 구하기를 Fenwick Tree를 이용해서 풀어봤습니다.
#include <cstdio>
#include <vector>
using namespace std;
long long sum(vector<long long> &tree, int i) {
long long ans = 0;
while (i > 0) {
ans += tree[i];
i -= (i & -i);
}
return ans;
}
void update(vector<long long> &tree, int i, long long diff) {
while (i < tree.size()) {
tree[i] += diff;
i += (i & -i);
}
}
int main() {
int n, m, k;
scanf("%d %d %d",&n,&m,&k);
vector<long long> a(n+1);
vector<long long> tree(n+1);
for (int i=1; i<=n; i++) {
scanf("%lld",&a[i]);
update(tree, i, a[i]);
}
m += k;
while (m--) {
int t1;
scanf("%d",&t1);
if (t1 == 1) {
int t2;
long long t3;
scanf("%d %lld",&t2,&t3);
long long diff = t3-a[t2];
a[t2] = t3;
update(tree, t2, diff);
} else {
int t2,t3;
scanf("%d %d",&t2,&t3);
printf("%lld\n",sum(tree, t3) - sum(tree, t2-1));
}
}
return 0;#!/usr/bin/env python3
"""
Binary Indexed Tree / Fenwick Tree
https://www.hackerearth.com/practice/notes/binary-indexed-tree-made-easy-2/
https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/
https://www.youtube.com/watch?v=v_wj_mOAlig
https://www.youtube.com/watch?v=kPaJfAUwViY
"""
def update(index, value, array, bi_tree):
"""
Updates the binary indexed tree with the given value
:param index: index at which the update is to be made
:param value: the new element at the index
:param array: the input array
:param bi_tree: the array representation of the binary indexed tree
:return: void
"""
while index < len(array):
bi_tree[index] += value
index += index & -index
def get_sum(index, bi_tree):
"""
Calculates the sum of the elements from the beginning to the index
:param index: index till which the sum is to be calculated
:param bi_tree: the array representation of the binary indexed tree
:return: (integer) sum of the elements from beginning till index
"""
ans = 0
while index > 0:
ans += bi_tree[index]
index -= index & -index
return ans
def get_range_sum(left, right, bi_tree):
"""
Calculates the sum from the given range
:param bi_tree: the array representation of the binary indexed tree
:param left: left index of the range (1-indexed)
:param right: right index of the range (1-indexed)
:return: (integer) sum of the elements in the range
"""
ans = get_sum(right, bi_tree) - get_sum(left - 1, bi_tree)
return ans
def main():
n = int(input('Enter the number of elements: '))
arr = [int(x) for x in input('Enter the {} elements of the array: '.format(n)).split()]
arr.insert(0, 0) # insert dummy node for 1-based indexing
bit = [0 for i in range(n+1)]
for index in range(1, n+1):
update(index, arr[index], arr, bit)
"""
For range sum queries
l, r = map(int, input('Enter the left and right indices for the range sum: ').split())
print(get_range_sum(l, r, bit))
For updating the binary indexed tree
update(index, new_value - arr[index], arr, bit)
"""
if __name__ == '__main__':
main()2차원 펙윅트리 구현
입력받은 배열은 아래와 같다.
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
첫번째 행부터 채워보자.

다음, 두번째 행을 채워보자.

다음, 세번째, 네번째 행을 바로 채워보자.
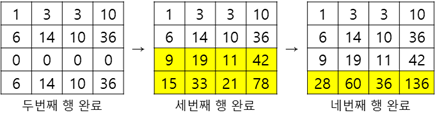
이를 확인해 보면, 오른쪽으로 펜윅트리가 동작함과 동시에, 아래쪽으로도 펜윅트리가 동작한다.
좀 더 구체적으로 설명하면, 아래 그림처럼 오른쪽으로 채워지는 펜윅트리의 각각의 열이 아래쪽으로 채워지고 있다.
 1행을 채우는 과정
1행을 채우는 과정
 2행을 채우는 과정
2행을 채우는 과정
쉽게 말해 while루프 중첩을 통해 오른쪽으로 더해지며, 이 값들이 아래쪽으로 더해지는 것이다.
따라서, sum 함수 또한 위 코드와 같이 while루프 중첩을 통해 합을 구할 수 있는 것이다.
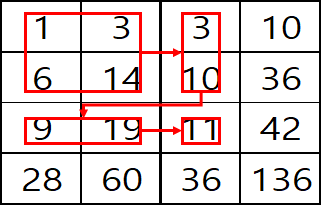 배열에서 (1,1) ~ (3,3) 의 합을 구할 경우 펜윅트리에서 위와 같은 순서로 동작
배열에서 (1,1) ~ (3,3) 의 합을 구할 경우 펜윅트리에서 위와 같은 순서로 동작
이를 통해 2차원 배열의 구간합을 구할 수 있는데, 방법은 간단하다.
아래와 같이 2차원 배열에서 (x1,y1) ~ (x2,y2) 구간합을 구하고자 한다.

이는 펜윅트리에서 아래와 같이 sum함수를 계산함으로써 그 값을 구할 수 있게 된다.
(마찬가지로 x축은 세로, y축은 가로로 설정하였다.)

(x1,y1)~(x2,y2)의 구간합 : sum(x2,y2) – sum(x1-1,y2) – sum(x2,y1-1) + sum(x1-1,y1-1)
지금까지 2차원 펜윅트리의 동작방식에 대해 구체적으로 살펴 보았다.
이를 이해한다면 3차원, 4차원 등 고차원 펜윅트리를 만드는 것 또한 쉽게 이해할 수 있을 듯 하다.
#include "sharifa_header.h"
class FenwickTree2D {
public:
int size;
vector<vector<long long> > data;
FenwickTree2D(int _N) {
size = _N;
data = vector<vector<long long> >(size + 1, vector<long long>(size + 1));
}
void update(int x, int y, int val) {
ll dval = val - sum(x, y, x, y);
int yy;
while (x <= size) {
yy = y;
while (yy <= size) {
data[x][yy] += dval;
yy += yy & -yy;
}
x += x & -x;
}
}
ll sum(int x, int y) {
ll ret = 0;
int yy;
while (x) {
yy = y;
while (yy) {
ret += data[x][yy];
yy -= yy & -yy;
}
x -= (x&-x);
}
return ret;
}
inline ll sum(int x1, int y1, int x2, int y2) {
return sum(x2, y2) - sum(x1 - 1, y2) - sum(x2, y1 - 1) + sum(x1 - 1, y1 - 1);
}
};3차원 펜윅트리
const int SIZE = 512;
bool init = 0;
const int SIZE_FW = SIZE + 1;
int fw[SIZE_FW][SIZE_FW][SIZE_FW];
int Sum(int x, int y, int z)
{
int res = 0;
for (int zz = z; zz > 0; zz -= (zz & -zz))
for (int yy = y; yy > 0; yy -= (yy & -yy))
for (int xx = x; xx > 0; xx -= (xx & -xx))
res += fw[zz][yy][xx];
return res;
}
int Sum(int xs, int xe, int ys, int ye, int zs, int ze)
{
int res = Sum(xe, ye, ze);
res -= Sum(xs - 1, ye, ze);
res -= Sum(xe, ys - 1, ze);
res -= Sum(xe, ye, zs - 1);
res += Sum(xs - 1, ys - 1, ze);
res += Sum(xs - 1, ye, zs - 1);
res += Sum(xe, ys - 1, zs - 1);
res -= Sum(xs - 1, ys - 1, zs - 1);
return res;
}
void Add(int x, int y, int z)
{
for (int zz = z; zz < SIZE_FW; zz += (zz & -zz))
for (int yy = y; yy < SIZE_FW; yy += (yy & -yy))
for (int xx = x; xx < SIZE_FW; xx += (xx & -xx))
fw[zz][yy][xx]++;
}
void Init(bool cube[SIZE][SIZE][SIZE])
{
init = 1;
memset(fw, 0, SIZE_FW * SIZE_FW * SIZE_FW * sizeof(int));
for (int z = 0; z < SIZE; z++)
for (int y = 0; y < SIZE; y++)
for (int x = 0; x < SIZE; x++)
if(cube[z][y][x])
Add(x + 1, y + 1, z + 1);
}
int CountDefect(bool cube[SIZE][SIZE][SIZE], int xs, int xe, int ys, int ye, int zs, int ze)
{
if (!init) Init(cube);
return Sum(xs+1, xe+1, ys+1, ye+1, zs+1, ze+1);
}펜윅트리로 최솟값 연산하는법(펜윅트리 양방향 두개 그리기.)
# fenwick
import sys
read = sys.stdin.readline
MAX = 1000000001
def update(i, x):
while i <= n:
tree[i] = min(tree[i], x)
i += (i & -i)
def update2(i, x):
while i > 0:
tree2[i] = min(tree2[i], x)
i -= (i & -i)
def query(a, b):
v = MAX
prev = a
curr = prev + (prev & -prev)
while curr <= b:
v = min(v, tree2[prev])
prev = curr
curr = prev + (prev & -prev)
v = min(v, arr[prev])
prev = b
curr = prev - (prev & -prev)
while curr >= a:
v = min(v, tree[prev])
prev = curr
curr = prev - (prev & -prev)
return v
n, m = map(int, read().split())
arr = [0] * (n+1)
tree = [MAX] * (n+2)
tree2 = [MAX] * (n+2)
for i in range(1, n+1):
arr[i] = int(read())
update(i, arr[i])
update2(i, arr[i])
for i in range(m):
a, b = map(int, read().split())
print(query(a, b))
'practivceAlgorithm > 자료구조&알고리즘' 카테고리의 다른 글
| [알고리즘] LCA(최소 공통 조상)과 sparse table (0) | 2021.08.09 |
|---|---|
| [알고리즘] 2차원 배열의 회전 (0) | 2021.08.08 |
| [자료구조] Segment Tree : 구간 연산 구간 변경 (0) | 2021.08.03 |
| [알고리즘] 비트마스크???!!! (0) | 2021.07.29 |
| [자료구조] 이진트리와 탐색. 파이썬의 bisect (0) | 2021.07.25 |